Leetcode: Unique Paths II

Unique Paths II

My Submissions

Total Accepted: 52512 Total Submissions: 184268 Difficulty: Medium

Follow up for "Unique Paths":

Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and empty space is marked as 1 and 0 respectively in the grid.

For example,

There is one obstacle in the middle of a 3x3 grid as illustrated below.

[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]

The total number of unique paths is 2.

Note: m and n will be at most 100.

Subscribe to see which companies asked this question

Hide Tags

 Array Dynamic Programming

Show Similar Problems

`````````````````````````````````````````````````````````````````````````

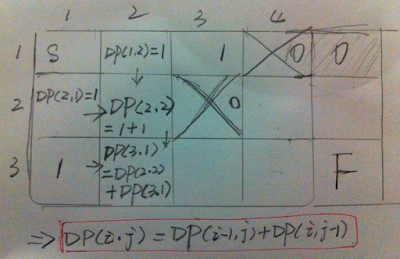
Based on the Unique Paths I, set all blocks with obstacles as 0 in DP, the others are the same. 

NOTE: The boundary blocks after a obstacles are all with value 0, e.g., the first row, the 4th block is an obstacle, so the value after the 4th block are all 0. 

///////////////////////////////////////////////////////////////////////

//codes

class Solution {

public:

    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {

        vector<vector<int>> dp=obstacleGrid;

        int lenR=obstacleGrid.size(), lenC=obstacleGrid[0].size();

        //set all val in dp to 0 for convient purpose

        for (int i=0;i<lenR;i++){

            dp[i].assign(lenC,0);  

        }

        //set val for all boundary as 1

        for (int i=0;i<lenR;i++){

            if(obstacleGrid[i][0]==0)dp[i][0]=1;

            else break;

        }

        for(int i=0;i<lenC;i++){

            if(obstacleGrid[0][i]==0)dp[0][i]=1;

            else break;

        }

        //calulate other values

        for(int i=1;i<lenR;i++){

            for(int j=1;j<lenC;j++){

                if(obstacleGrid[i][j]==1)continue;

                else dp[i][j]=dp[i-1][j]+dp[i][j-1];

            }

        }

        return dp[lenR-1][lenC-1];

    }

};